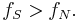Nyquist rate

Not to be confused with Nyquist frequency.

In signal processing, the Nyquist rate, named after Harry Nyquist, is two times the bandwidth of a bandlimited signal or a bandlimited channel. This term is used to mean two different things under two different circumstances:

  1. as a lower bound for the sample rate for alias-free signal sampling[1] (not to be confused with the Nyquist frequency, which is half the sampling rate of a discrete-time system) and
  2. as an upper bound for the symbol rate across a bandwidth-limited baseband channel such as a telegraph line[2] or passband channel such as a limited radio frequency band or a frequency division multiplex channel.

Contents

Nyquist rate relative to sampling

The Nyquist rate is the minimum sampling rate required to avoid aliasing, equal to twice the highest frequency contained within the signal.

f_N \ \stackrel{\mathrm{def}}{=}\ 2 B\,

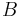where B\, is the highest frequency at which the signal can have nonzero energy.

To avoid aliasing, the sampling rate must exceed the Nyquist rate:

f_S > f_N.\,

A signal whose positive-frequency range of significant energy is (0, B), as depicted above, is called baseband or lowpass. But when the frequency range is (A, B), for some A > B − A, it is called bandpass. In that case, aliasing is not necessarily detrimental, and sampling below the Nyquist rate, called bandpass sampling, is sometimes done. With careful design, a rate as low as 2(B − A) may be achievable, and it is equivalent to mixing (heterodyne) the signal into the frequency range (0, B − A), whose Nyquist rate is 2(B − A). An even lower Nyquist rate can be achieved for a bandpass signal, such as amplitude modulation, whose energy distribution in (A, B) is symmetrical. In that case, the homodyne mixer translates the signal frequencies by (A + B)/2, with a synchronized phase, which moves the highest component to (B − A)/2 and the Nyquist rate to just (B − A).

Nyquist rate relative to signaling

Long before Harry Nyquist had his name associated with sampling, the term Nyquist rate was used differently, with a meaning closer to what Nyquist actually studied. Quoting Harold S. Black's 1953 book Modulation Theory, in the section Nyquist Interval of the opening chapter Historical Background:

"If the essential frequency range is limited to B cycles per second, 2B was given by Nyquist as the maximum number of code elements per second that could be unambiguously resolved, assuming the peak interference is less half a quantum step. This rate is generally referred to as signaling at the Nyquist rate and 1/(2B) has been termed a Nyquist interval." (bold added for emphasis; italics as in the original)

According to the OED, this may be the origin of the term Nyquist rate.[3]

Nyquist's famous 1928 paper was a study on how many pulses (code elements) could be transmitted per second, and recovered, through a channel of limited bandwidth. Signaling at the Nyquist rate meant putting as many code pulses through a telegraph channel as its bandwidth would allow. Shannon used Nyquist's approach when he proved the sampling theorem in 1948, but Nyquist did not work on sampling per se.

Black's later chapter on "The Sampling Principle" does give Nyquist some of the credit for some relevant math:

"Nyquist (1928) pointed out that, if the function is substantially limited to the time interval T, 2BT values are sufficient to specify the function, basing his conclusions on a Fourier series representation of the function over the time interval T."

See also

References

  1. ^ Yves Geerts, Michiel Steyaert, and Willy Sansen (2002). Design of multi-bit delta-sigma A/D converters. Springer. ISBN 1402070780. http://books.google.com/books?id=99nwX-ovq7QC&pg=PA15&dq=nyquist-rate+define+bandwidth+sampling#PPA14,M1. 
  2. ^ Roger L. Freeman (2004). Telecommunication System Engineering. John Wiley & Sons. pp. 399. ISBN 0471451339. http://books.google.com/books?id=Ga7PYE7E8kQC&pg=PA399&dq=nyquist-rate+define+bandwidth+symbols. 
  3. ^ Black, H. S., Modulation Theory, v. 65, 1953, cited in OED
Theory
Sub-fields
Techniques
Sampling